2015, Robotics and Mechanism Laboratory, UCLA
Using MSC Adams and MATLAB co-simulation, an optimization of gait motion of a hexapod robot was conducted. In order to develop agile and energy efficient walking motion, genetic algorithm optimization was introduced to the iterative dynamic simulations with MSC Adams. The CAD Model of hexapod robot was generated and imported to MSC Adams. The hexapod robot has 18 motors on its each joints. In order to do dynamic simulation, not kinematic, the motor torque was modeled based on a torque-speed relationship. A motor position controller was simulated in MATLAB so that the motor torque was calculated with the input voltage from the controller.
Mov 1. The simulation model of a hexapod robot in MSC Adams
The optimization process was conducted by a genetic algorithm. The model characterized by genes evolves as generation progresses. In every change of generation, genes are evaluated, only high-scored ones are selected, and they are populated to fill the next generation while mutation and crossover occurs to make diversity. Since the genetic algorithm requires iterations, MSC Adams is perfectly fit to apply genetic algorithm to a precise simulation model. In addition, due to the randomly generated initial genotypes, it is almost impossible to apply genetic algorithm to a real hardware, but appropriate for dynamic simulation.
Fig 1. Foot Trajectory Defined in Polar Coordinate System
Since a hexapod gain motion is periodic motion that every foot has same trajectory but has different phase, the optimization was focused on developing an optimal foot trajectory for one step. The genes are comprised of twenty-four genotypes, and each genotype stands for the position of a foot at a moment which is expressed in polar coordinate when the origin is the initial position of the foot. The foot trajectory is converted to joint angle sequence by inverse kinematics and the motors were controlled to follow the joint angle sequence. Each gene is evaluated by a fitness function that is decided velocity of the COM of a robot and sum of every motor torque are used as output signals.
Each generation had thirty populations, and each population was independently simulated. After each simulation, each gene was evaluated with a designated function and high scored genes were selected. Only 10% of top-scored genes survive and generated genes of a new generations through a cross-over and mutation process. The mutation and crossover help the process may include broader cases. Forty generations are used in given simulation.
Fig 2. The result of joint angle sequence
As generations progresses during the genetic algorithm, the joint angle sequence are converged as those in the plot. The best score in each generation was increased and converged, which can be considered the algorithm was properly worked. The comparison between the foot trajectory of initial simulation and final simulation is shown in the figure below.
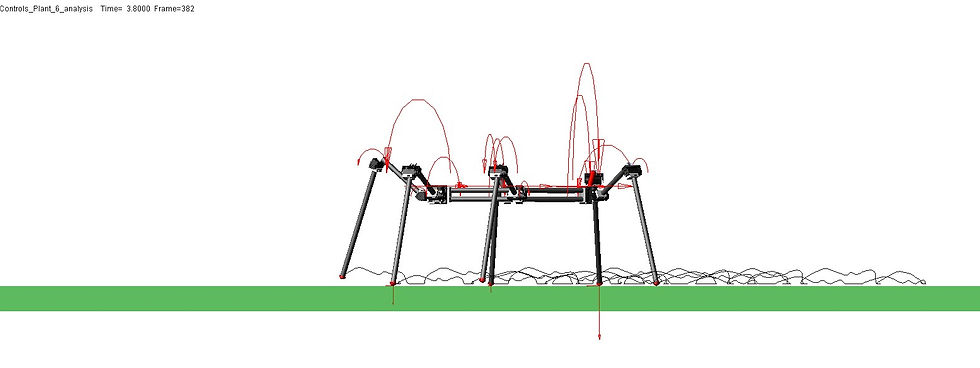
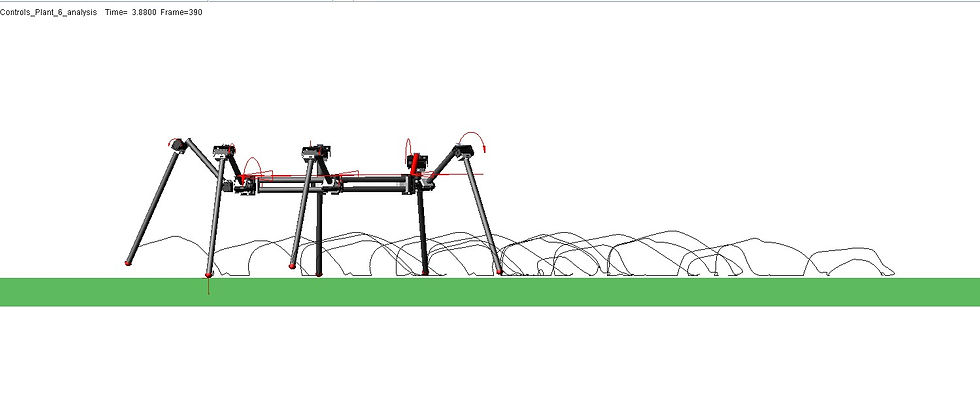
Fig 3. Foot trajectories of the best scored gene of initial generation(Up) and final generation(down)